Haben Sie schon einmal mit Ihrem Smartphone Fotos gemacht?
Wenn wir den iPhone-Bildsensor analysieren, können wir die Entwicklung der Smartphone-Kameras gut nachvollziehen. Der Sony IMX503 ist einer der Bildsensoren, die in der iPhone-Kamera verwendet werden. Daher möchten wir in diesem Artikel den Bildsensor des iPhone 12 untersuchen, wobei wir auch Messmethoden in einem Dunkelraum einbeziehen.
Warum den iPhone-Bildsensor analysieren?
Es ist schon eine Weile her, dass das Smartphone seinen Weg in die Welt gefunden hat. Doch die Kamerafunktionen haben sich erstaunlich weiterentwickelt. Es ist jedoch auch wahr, dass es immer noch eine Leistungslücke im Vergleich zu Spiegelreflexkameras gibt, wenn es um Aufnahmen in dunklen Umgebungen geht. Trotzdem, bei gut beleuchteten Szenen können Smartphones mittlerweile so schöne Fotos machen, dass man eine Spiegelreflexkamera dafür nicht mehr benötigt.
Da das Smartphone, insbesondere das iPhone, ein Gerät ist, das wir im Alltag ständig nutzen, ist die Analyse des iPhone-Bildsensors von großer Bedeutung.
Bildsensor im iPhone 12
Mein aktuelles Smartphone ist das iPhone 12 (Standardmodell). Daher wird der Bildsensor des iPhone 12 als Analyseobjekt verwendet.
Trotz intensiver Recherche konnte ich jedoch kein Datenblatt für den Bildsensor finden. Wahrscheinlich handelt es sich um einen speziell für Apple entwickelten Sensor, der nicht als kommerzielles Produkt veröffentlicht wurde. Allerdings gibt es sicherlich viele, die an der Leistung dieses Sensors interessiert sind, und deshalb ist es durchaus wert, eine Analyse des iPhone-Bildsensors zu versuchen.
Messmethoden für den Bildsensor
In dieser Analyse werden wir die Ausgabeantwort und die Rauschleistung des Bildsensors untersuchen. Zunächst einmal sind die folgenden Geräte und Materialien für die Messung erforderlich:
- iPhone (mit einer Kamera-App, die Raw-Bilder aufnehmen kann)
- ND-Filter mit 15 Blendenstufen
- Flache Lichtquelle
- Dunkler Raum
- PC (mit Python)
Messpunkte
Messung im Dunkelraum:
Es ist wichtig sicherzustellen, dass kein zusätzliches Licht in den Raum gelangt, um die Linearity in den dunklen Bereichen korrekt zu messen.
Raw-Bilderfassung:
Mit der Standard-iPhone-Kamera-App können keine Raw-Bilder aufgenommen werden. Mit einer App wie der „SimpleRaw Camera“ ist es jedoch möglich, Raw-Aufnahmen im DNG-Dateiformat zu machen.
Flache Lichtquelle:
Verwenden Sie eine möglichst gleichmäßige Lichtquelle, um eine gleichmäßige Helligkeit zu gewährleisten. Wenn Sie über eine Integralsphäre verfügen, können Sie diese direkt verwenden. Andernfalls können Sie auch einen PC-Monitor verwenden, den Sie auf weiß setzen und auf maximale Helligkeit einstellen.
ND-Filter:
Ein ND-Filter (Neutraldichte-Filter) ist notwendig, um die Lichtmenge zu reduzieren. Wenn kein Filter vorhanden ist, können Sie auch die Belichtungszeit anpassen, aber beachten Sie, dass sich dadurch möglicherweise die Rauschcharakteristiken ändern.
Messverfahren
- Fixieren der Position von Lichtquelle und Kamera:
Stellen Sie sicher, dass sowohl die Lichtquelle als auch die Kamera in einer festen Position sind. (Achten Sie darauf, genügend Arbeitsraum zu haben, um alle ND-Filter einzusetzen.) - Erhöhen der Helligkeit der Lichtquelle:
Machen Sie die Lichtquelle so hell, dass die Kamera ohne ND-Filter in den Sättigungsbereich geht. Wenn die Lichtquelle nicht ausreicht, um die Kamera zu sättigen, versuchen Sie, die Belichtungszeit zu verlängern. - Aufnahme der Lichtquelle:
Fotografieren Sie die Lichtquelle und reduzieren Sie dann die Lichtmenge schrittweise um die Hälfte. Wiederholen Sie den Aufnahmeprozess.
Es gibt zwei Methoden, um die Lichtmenge zu verringern: Sie können entweder einen ND-Filter nach dem anderen hinzufügen oder die Belichtungszeit anpassen. - Datenaufnahme abschließen:
Sobald Sie von der Sättigung bis zu einem ausreichend dunklen Zustand aufgenommen haben, ist die Datenerfassung abgeschlossen.
Wichtig: Ändern Sie nicht die Entfernung zwischen Lichtquelle und Kamera.
Wenn sich die Entfernung verändert, ändert sich auch die Lichtmenge, was zu ungenauen Ergebnissen führen würde.
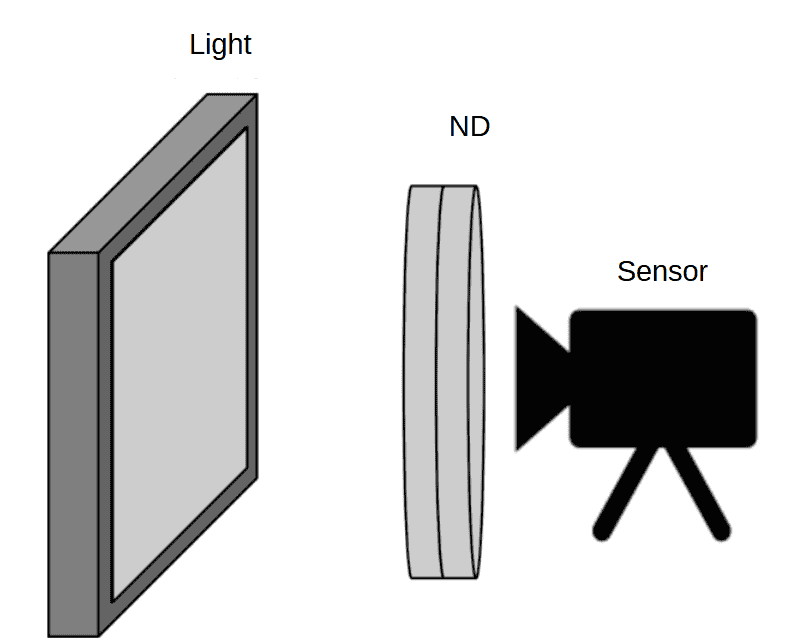
Tatsächliche Anordnung
Bereiten Sie einen dunklen Raum oder einen dunklen Bereich vor und platzieren Sie den ND-Filter zwischen der Kamera (iPhone) und der Lichtquelle.
Achten Sie darauf, dass weder der Filter noch die Kamera bewegt werden, da dies die Messbedingungen verändern könnte. Daher müssen sowohl der Filter als auch die Kamera fest fixiert werden.
Analyse der Raw-Daten
Nun werden wir die aufgenommenen Raw-Daten analysieren. Allerdings haben sowohl iPhones, die DNG-Dateien verwenden, als auch Spiegelreflexkameras oft proprietäre Formate. Daher ist es sinnvoll, die Raw-Daten zunächst in ein universelles Raw-Format umzuwandeln, bevor wir sie mit Python weiterverarbeiten.
Hier ist der tatsächliche Analysecode. Wir verwenden Python zusammen mit den Bibliotheken Numpy, Matplotlib und Math:
import numpy as np
import matplotlib.pyplot as plt
import math
#***********************************
#1.setup
#***********************************
width=4032
height=3024
width_roi = 100
height_roi = 100
image_num = 15
bit = 12
dark = 528 #
half_width = int(width/2)
half_height = int(height/2)
half_width_roi = int(width_roi/2)
half_height_roi = int(height_roi/2)
#***********************************
#2.array
#***********************************
img_roi=np.empty((height_roi, width_roi),dtype = np.uint16)
img_s = np.empty((4,image_num),dtype = np.float32)
img_n = np.empty((4,image_num),dtype = np.float32)
img_sn = np.empty((4,image_num),dtype = np.float32)
rgb = np.array(range(4))
rgb_det = rgb.reshape((2,2))
img_roi_r=np.empty((half_height_roi, half_width_roi),dtype = np.uint16)
img_roi_gr=np.empty((half_height_roi, half_width_roi),dtype = np.uint16)
img_roi_gb=np.empty((half_height_roi, half_width_roi),dtype = np.uint16)
img_roi_b=np.empty((half_height_roi, half_width_roi),dtype = np.uint16)
x_axis = np.empty((1,image_num),dtype = np.uint16)
#***********************************
#3.Raw
#***********************************
for i in range(image_num):
x_axis[0][i] = 2**i
rawpath = "DNG_4032x3024_dark=528_12bit_lin"+str(i)+".raw"
#***********************************
#raw
#***********************************
fd = open(rawpath, 'rb')
f = np.fromfile(fd, dtype=np.uint16, count=height*width)
img = f.reshape((height,width))
fd.close()
#***********************************
#ROI
#***********************************
width_roi_start = int((width-width_roi)/2)
height_roi_start = int((height-height_roi)/2)
for x in range(width_roi_start,width_roi_start+width_roi):
for y in range(height_roi_start,height_roi_start+height_roi):
img_roi[y-height_roi_start][x-width_roi_start] = img[y][x]
#***********************************
#Dark
#***********************************
for x in range(width_roi):
for y in range(height_roi):
if img_roi[y][x] > dark:
img_roi[y][x] = img_roi[y][x]-dark
else:
img_roi[y][x] = 0
#***********************************
#SN
#***********************************
for x in range(width_roi):
for y in range(height_roi):
color = rgb_det[y % 2][x % 2]
if color == 0: #R
y_r = int(y/2)
x_r = int(x/2)
img_roi_r[y_r][x_r] = img_roi[y][x]
elif color == 1: #Gr
y_gr = int(y/2)
x_gr = int((x-1)/2)
img_roi_gr[y_gr][x_gr] = img_roi[y][x]
elif color == 2: #Gb
y_gb = int((y-1)/2)
x_gb = int(x/2)
img_roi_gb[y_gb][x_gb] = img_roi[y][x]
else: #B
y_gb = int((y-1)/2)
x_gb = int((x-1)/2)
img_roi_b[y_gb][x_gb] = img_roi[y][x]
img_s[0][i] = np.mean(img_roi_r)
img_s[1][i] = np.mean(img_roi_gr)
img_s[2][i] = np.mean(img_roi_gb)
img_s[3][i] = np.mean(img_roi_b)
img_n[0][i] = np.std(img_roi_r)
img_n[1][i] = np.std(img_roi_gr)
img_n[2][i] = np.std(img_roi_gb)
img_n[3][i] = np.std(img_roi_b)
img_sn[0][i] = 20*(math.log10(img_s[0][i]/img_n[0][i]))
img_sn[1][i] = 20*(math.log10(img_s[1][i]/img_n[1][i]))
img_sn[2][i] = 20*(math.log10(img_s[2][i]/img_n[2][i]))
img_sn[3][i] = 20*(math.log10(img_s[3][i]/img_n[3][i]))
fig1 = plt.figure()
ax1 = fig1.add_subplot(111)
ax1.plot(x_axis[0,:], img_sn[0,:],label = "R",color = "r")
ax1.plot(x_axis[0,:], img_sn[1,:],label = "Gr",color = "lightgreen")
ax1.plot(x_axis[0,:], img_sn[2,:],label = "Gb",color = "forestgreen")
ax1.plot(x_axis[0,:], img_sn[3,:],label = "B",color = "b")
ax1.set_xscale("log")
ax1.legend()
fig2 = plt.figure()
ax2 = fig2.add_subplot(111)
ax2.plot(x_axis[0,:], img_s[0,:],label = "R",color = "r")
ax2.plot(x_axis[0,:], img_s[1,:],label = "Gr",color = "lightgreen")
ax2.plot(x_axis[0,:], img_s[2,:],label = "Gb",color = "forestgreen")
ax2.plot(x_axis[0,:], img_s[3,:],label = "B",color = "b")
ax2.plot(x_axis[0,:], img_n[0,:],linestyle="--",label = "R_Noise",color = "r")
ax2.plot(x_axis[0,:], img_n[1,:],linestyle="--",label = "Gr_Noise",color = "lightgreen")
ax2.plot(x_axis[0,:], img_n[2,:],linestyle="--",label = "Gb_Noise",color = "forestgreen")
ax2.plot(x_axis[0,:], img_n[3,:],linestyle="--",label = "B_Noise",color = "b")
ax2.set_xscale("log")
ax2.set_yscale("log")
ax2.legend()
plt.show()
Entschuldigung für das Missverständnis. Hier ist die Übersetzung:
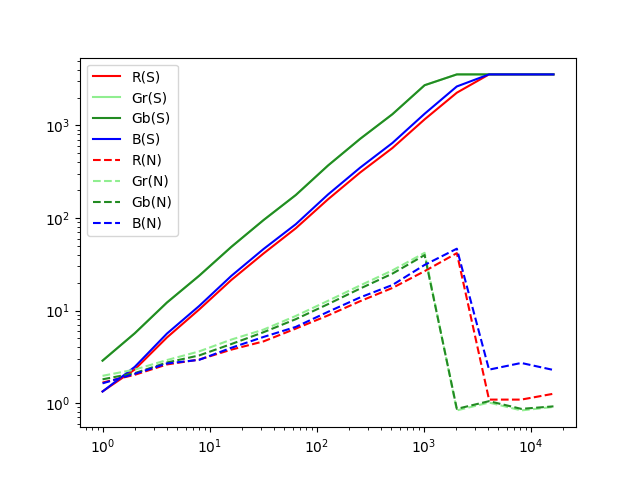
Wenn der Code ausgeführt wird, werden Diagramme angezeigt. Eines zeigt die Signal- und Rauschantwortmerkmale, das andere die SN-Verhältnismerkmale.
Analyseergebnisse und Betrachtung
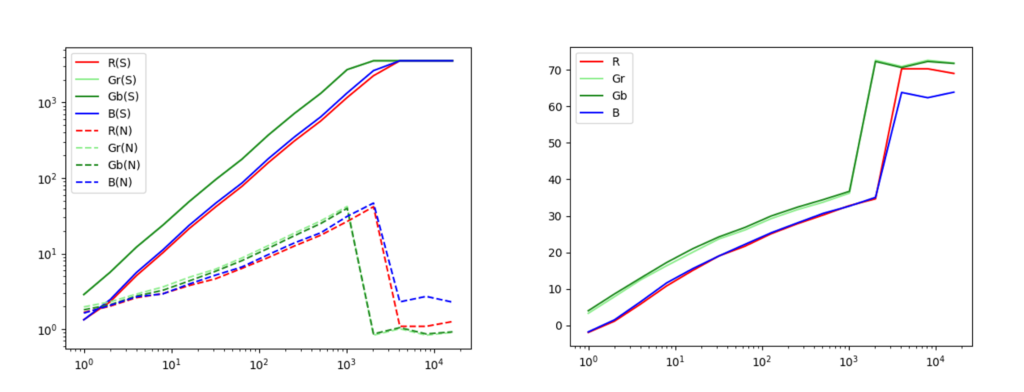
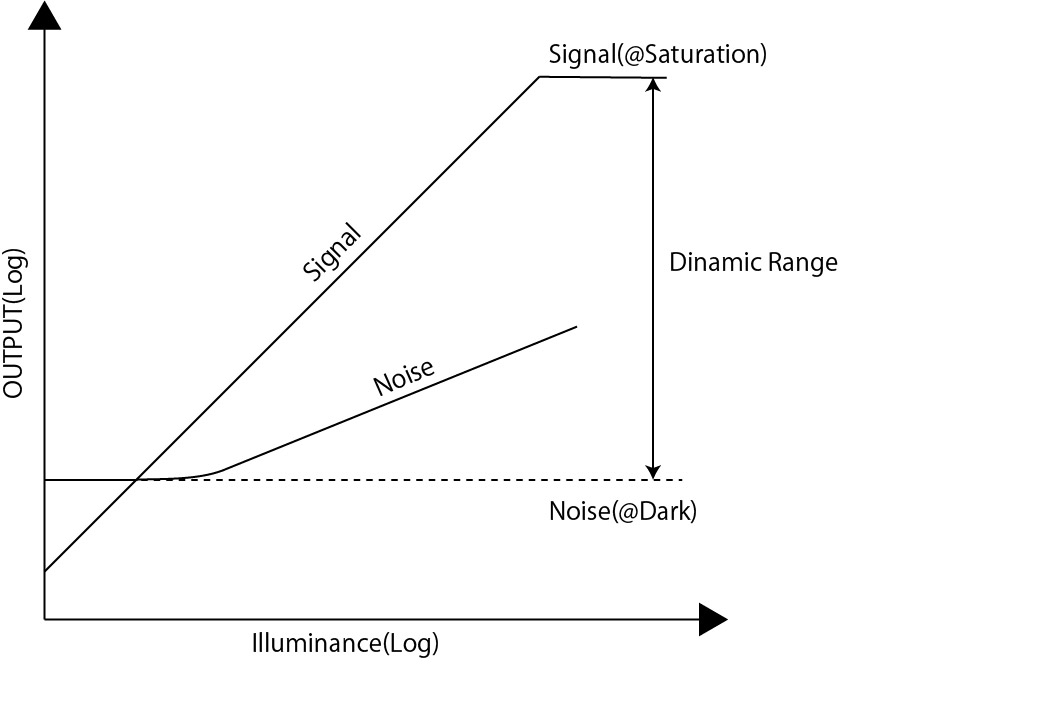
Das Signal ist proportional zur Lichtmenge
Wie zu erwarten, steigt die Sensorausgabe mit zunehmender Lichtmenge.
Das Rauschen ist nahezu proportional zur Quadratwurzel des Signals
Dies ist eine typische Eigenschaft des Shot Noise (Photonenrauschen).
Das Signal-Rausch-Verhältnis (SN-Verhältnis) beträgt maximal etwa 35 dB
Außerdem liegt der dynamische Bereich bei etwa 70 dB.
Das bedeutet, dass die groben Merkmale des IMX503 Sensors, der im iPhone 12 verbaut ist, aus diesen Ergebnissen abgeleitet werden können. Diese Methode ist jedoch nicht nur auf das iPhone beschränkt, sondern kann auf alle Kameras angewendet werden. Versuchen Sie ruhig, diese Methode mit den Kamerasensoren Ihrer eigenen Geräte auszuprobieren.
Zusammenfassung: Die Faszination der iPhone-Bildsensor-Analyse
In diesem Artikel haben wir eine konkrete Methode zur Analyse des iPhone-Bildsensors vorgestellt. Durch die Verwendung von Dunkelraummessungen, ND-Filtern und Raw-Datenanalysen mit Python können die Eigenschaften des Sony IMX503 Sensors untersucht werden. Es ist auch sehr interessant, die Leistungssteigerung der Smartphone-Kamera anhand von quantitativen Daten zu überprüfen.
Für diejenigen, die die Leistung ihrer alltäglichen Smartphone-Kamera näher untersuchen möchten, empfehlen wir, mit derselben Methode eigene Daten zu sammeln und zu analysieren. Im Vergleich zu Spiegelreflexkameras oder spiegellosen Kameras wird der Leistungsunterschied noch deutlicher und spannend.
Wichtig: Für alle Phänomene oder Schäden, die durch die Verwendung dieses Codes auftreten, übernehmen wir keine Verantwortung. Bitte nutzen Sie die Informationen ausschließlich als Referenz.

コメント